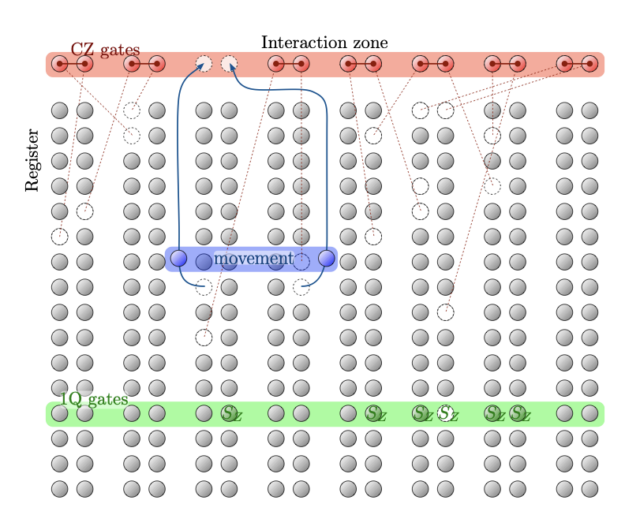
Atom Computing’s system. Rows of atoms are held far enough apart so that a single laser sent across them (green bar) only operates on individual atoms. If the atoms are moved to the interaction zone (red bar), a laser can perform gates on pairs of atoms. Spaces where atoms can be held can be left empty to avoid performing unneeded operations.
Credit:
Reichardt, et al.
The machine used in the new demonstration hosts 256 of these neutral atoms. Atom Computing has them arranged in sets of parallel rows, with space in between to let the atoms be shuffled around. For single-qubit gates, it’s possible to shine a laser across the rows, causing every atom it touches to undergo that operation. For two-qubit gates, pairs of atoms get moved to the end of the row and moved a specific distance apart, at which point a laser will cause the gate to be performed on every pair present.
Atom’s hardware also allows a constant supply of new atoms to be brought in to replace any that are lost. It’s also possible to image the atom array in between operations to determine whether any atoms have been lost and if any are in the wrong state.
It’s only logical
As a general rule, the more hardware qubits you dedicate to each logical qubit, the more simultaneous errors you can identify. This identification can enable two ways of handling the error. In the first, you simply discard any calculation with an error and start over. In the second, you can use information about the error to try to fix it, although the repair involves additional operations that can potentially trigger a separate error.
For this work, the Microsoft/Atom team used relatively small logical qubits (meaning they used very few hardware qubits), which meant they could fit more of them within 256 total hardware qubits the machine made available. They also checked the error rate of both error detection with discard and error detection with correction.
The research team did two main demonstrations. One was placing 24 of these logical qubits into what’s called a cat state, named after Schrödinger’s hypothetical feline. This is when a quantum object simultaneously has non-zero probability of being in two mutually exclusive states. In this case, the researchers placed 24 logical qubits in an entangled cat state, the largest ensemble of this sort yet created. Separately, they implemented what’s called the Bernstein-Vazirani algorithm. The classical version of this algorithm requires individual queries to identify each bit in a string of them; the quantum version obtains the entire string with a single query, so is a notable case of something where a quantum speedup is possible.

